前言

之前(https://ithelp.ithome.com.tw/articles/10330192)我們有稍微提到AlexNet利用了與以往不同的激勵函數來避免梯度消失的問題，不過那時並沒有詳細的說明甚麼是激勵函數，以及梯度消失是甚麼問題，今天就讓我們來回答這些疑惑！

先備知識

1. 知道甚麼是反向傳播(可以回顧：https://ithelp.ithome.com.tw/articles/10324192)
2. 知道甚麼是梯度下降法(可以回顧https://ithelp.ithome.com.tw/articles/10318660 )

看完今天的內容你可能會知道......

1. 甚麼是梯度爆炸與梯度消失
2. 要如何避免梯度爆炸與梯度消失
3. 甚麼是激勵函數
4. 激勵函數可以起到甚麼樣的作用

一、梯度爆炸(Exploding gradient)與梯度消失(Vanishing gradient)

• 我們在https://ithelp.ithome.com.tw/articles/10324192 這邊有介紹到模型更新的方式是使用反向傳播法，由最靠近輸出結果的部分開始更新，一路把誤差資訊傳遞下去，一部部更新每一層的參數。
• 熟悉微積分的同學應該知道「連鎖律」，如果今天有個參數C與B相關，而B又與A相關，那麼我需要知道C跟A之間的關聯性，就需要將C與B的關聯性乘上B與A的關聯性，這就是連鎖律的核心概念。現在問題來了，在AI模型中，動輒就是好幾層、好幾百層，如果我要從最後一層往前計算關聯性的話，每傳遞一層就會需要乘上一大堆東西。所以可以想像，如果今天某個東西特別小的話，一路傳下去就會越乘越小，而且這個往下遞減趨勢非常快速，相反的如果這個傳遞的過程中突然有些東西特別大，一路乘下去大家都會變得非常大。
• 前者就是所謂的「梯度消失(Vanishing gradient)」現象，當誤差資訊因為這樣的原因而消失時(乘上小於1的數的話，越乘就會越靠近0)，就無法有效地更新所有的模型參數(梯度都是0的話，使用梯度下降法只會得到原先的參數值，所以無法更新參數)。而且這個現象會導致模型當中前後層的學習效果不一樣，這個很好想像，因為越傳遞到後來就會越沒有資訊，所以只有靠近輸出的那幾層可以正確地更新。
• 後者則是所謂的「梯度爆炸(Exploding gradient)」，與梯度消失相反，梯度爆炸是因為乘上了大於1的數，但是因為是相乘的關係，所以會瘋狂地放大。和梯度消失一樣，這個現象會使模型當中前後層的學習效果不一樣，不過這次是導致越靠近輸入的那幾層更新速度非常的快，這樣會使得模型的輸出結果瘋狂的震盪。
• 總而言之，梯度消失會導致模型比較前面的層無法有效更新，所以模型的表現會下降，而梯度爆炸的話則是導致比較前面的層不斷震盪，無法產生穩定的模型輸出結果。
• 除了調整模型本身的架構以外，為了避免這樣的現象，另一個很直覺的想法就是：既然傳遞的過程當中出現大於1或是小於1很容易出問題，那麼我能不能設計一個函數，在誤差傳遞的過程中避免這些問題？這就是下面我們會介紹的激勵函數的其中一個用途！
• 當然還有別的方式可以避免梯度消失與梯度爆炸，因為計算梯度時，除了考慮函數的輸出結果以外，跟你送進去函數的值也有關係，所以可以通過調整送入函數的值來避免，這樣的想法就是所謂的Batch Normalization，可以讓輸入函數的數值不要產生太大的波動。還有一種想法是出自梯度下降法的公式本身，我們在使用梯度下降法時，會將原先的參數值減去學習率(Learning rate)乘上梯度，所以我可以調整學習率來避免更新的結果受到太多梯度的影響。感興趣的可以參考：https://www.analyticsvidhya.com/blog/2021/06/the-challenge-of-vanishing-exploding-gradients-in-deep-neural-networks/

二、激勵函數(Activation Function)--誰給的激勵？又是要激勵誰？

• 在MLP的討論中(https://ithelp.ithome.com.tw/articles/10322151)，我們有提到激勵函數的靈感來源，一來是模擬生物神經元的運作方式，二來，在數學中，我們很難用「完全線性的模型」來預測真實世界的問題，所以我們需要加點魔法進去，這個魔法就是「非線性」，也就是激勵函數帶來的好處。

• 如果不清楚甚麼是線性甚麼是非線性的話，可以稍微想一下一個畫面：你在一張空白紙上隨便點很多個黑點，接下來你需要使用一條直線跟一條會彎曲的線，將所有黑點分成兩個區塊，直線對應的就是「線性」，會彎曲的線對應的就是「非線性」。從這個例子中我們可以看出來，現實世界中有許多問題都是非線性的，所以如果一個線性模型只能產生線性的結果的話，很難處理現實世界中的問題。

• 之前我們提到激勵函數的時候都是以概念為主，現在讓我們就著公式與函數圖形仔細的研究一下吧！

• 激勵函數一般有幾個特徵：非線性與可微分，前者上面說明過了，後者是因為激勵函數也是模型當中的一員，所以如果利用反向傳播(梯度下降)更新參數的時候，這個更新的資訊也會經過激勵函數，因此需要計算激勵函數的微分。

• 激勵函數可以按照其函數特性分成飽和激勵函數與非飽和激勵函數，主要的分類依據在於是否會隨著輸入訊號的改變而使函數的輸出值飽和。非飽和函數相較於飽和函數，除了可以加速模型的收斂速度以外，也可以避免梯度消失的問題，這個我們下面會解釋。除了飽和與非飽和以外，我們還可以關注這個激勵函數的輸出結果是否是以0為中心的對稱函數，如果不是的話，可能會使模型參數更新時產生額外的偏差(Bias)。

  1. Sigmoid

  • 
  • 又稱邏輯函數(Logisitc function)，輸出訊號的區間為(0,1)，當輸入訊號越大，輸出結果就會越靠近1，反之會越靠近0，所以這個函數是「飽和激勵函數」。可以參考：https://zh.wikipedia.org/zh-tw/%E9%80%BB%E8%BE%91%E6%96%AF%E8%B0%9B%E5%87%BD%E6%95%B0 ，最常在應用在分類任務中，讓我們針對每張輸入圖像都可以計算出屬於每個類別的機率，最後模型的預測結果就會是機率最高的類別。
  • 正如我們上面介紹到的，因為這個函數是飽和函數的關係，如果模型訓練到後來，一但有個參數以及要更新的值很小時，這個參數往下傳遞的訊號就會越來越小，導致模型的所有參數沒辦法很好的更新(梯度消失現象)。

  2. Tanh

  • 
  • 是比較早期的激勵函數，相較於Sigmoid來說，因為輸出結果的平均是0，所以避免的偏差(Bias)問題，但是也會面臨因為飽和引起得梯度消失現象。

  3. ReLU (Rectified Linear Unit) 與Leaky ReLU

  • 
  • 因其可以保留大於0的訊號而捨去其餘訊號，在訊號處理領域中是很常使用的「整流器」，可以參考：https://en.wikipedia.org/wiki/Rectifier_(neural_networks)
  • 這個函數的左邊會飽和，可是右邊不會，所以AlexNet中才會選擇使用ReLU，就是為了避免梯度消失的問題且可以提升模型的訓練速度。但是這樣的函數同樣會因為對稱中心不在0而產生偏差(Bias)現象，此外，如果模型訓練號後來，有許多訊號都是小於0的話，還是會因為落入飽和區使模型的所有參數無法有效地更新。
  • 所以，有人為了改善這樣的問題，提出了改良版的ReLU函數：，主要是處理左邊會飽和的問題。

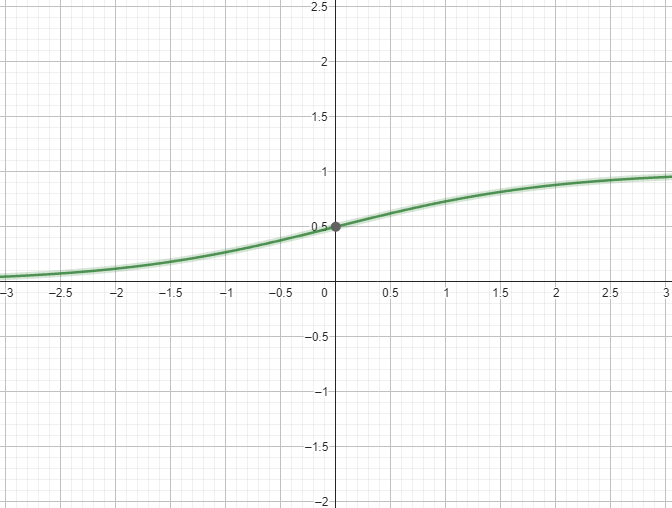
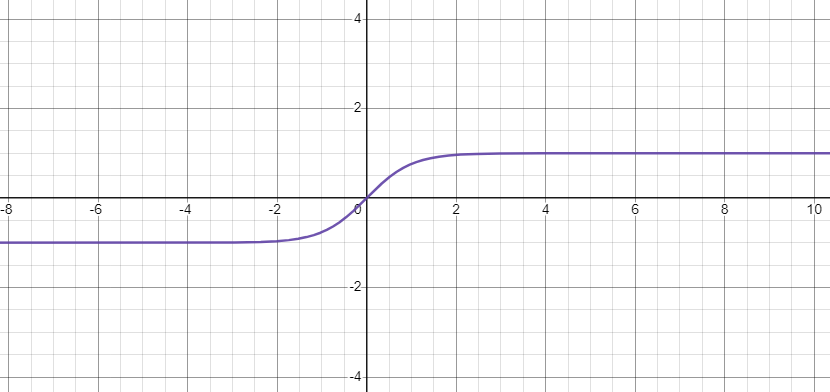
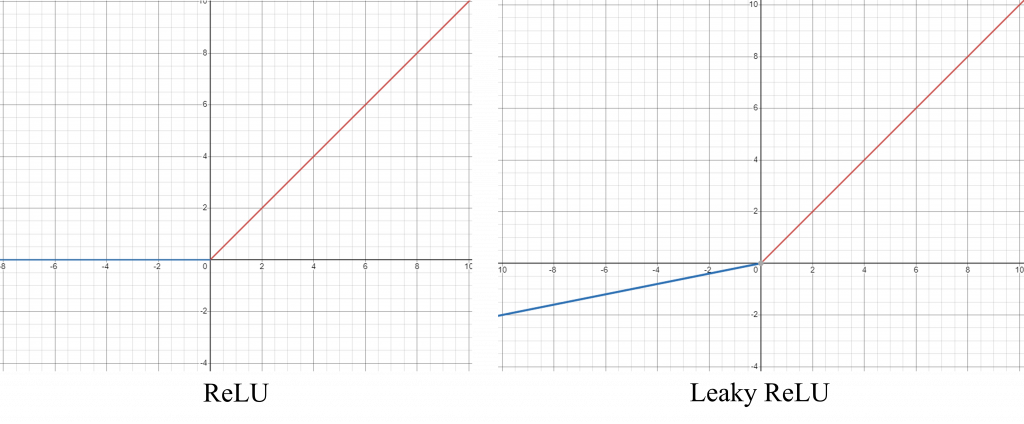
• 這邊提供了常見激勵函數的列表可以參考：https://zh.wikipedia.org/zh-tw/%E6%BF%80%E6%B4%BB%E5%87%BD%E6%95%B0 ，大家可以觀察一下每個函數的值域與定義域，並且看一下每個函數的微分長甚麼樣，值得注意的一點是，我們通常不太使用太複雜的激勵函數，因為這樣我們可能會需要話很多時間計算激勵函數與他的微分結果，會導致訓練時間變長。

三、總結

• 今天我們介紹了AI模型中的一個關鍵因素：激勵函數，並且分享了幾個常見的激勵函數，同時我們也說明了甚麼是梯度消失與梯度爆炸的現象，以及這樣的問題要如何透過激勵函數避免。